Signed number representation. Floating point format. Why is complementary code used to represent negative numbers?
Service purpose... The online calculator is designed to represent real numbers in floating point format.Number entry rules
- Numbers in the decimal notation system can be entered both without a fractional part, or with a fractional part (234234.455).
- Binary numbers only consist of the digits 0 and 1 (10100.01).
- Hexadecimal numbers consist of the digits 0 ... 9 and the letters A ... F.
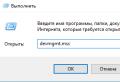
- You can also get the reverse representation of the code (from hexadecimal to decimal, 40B00000)
Decision... Let's represent the number 133.54 in normalized exponential form:
1.3354 * 10 2 \u003d 1.3354 * exp 10 2
The number 1.3354 * exp 10 2 consists of two parts: the mantissa M \u003d 1.3354 and the exponent exp 10 \u003d 2
If the mantissa is in the range 1 ≤ M Denormalized exponential representation of a number.
If the mantissa is in the range 0.1 ≤ M Let's represent the number in denormalized exponential notation: 0.13354 * exp 10 3
Example # 2. Represent the binary number 101.10 2 in normalized form, write it down in the 32-bit IEEE754 standard.
Decision.
Exponential Normalized Binary Floating Point Representation.
Let's shift the number 2 places to the right. As a result, we got the main components of the exponential normalized binary number:
Mantissa M \u003d 1.011
Exponent exp 2 \u003d 2
Convert normalized binary number to 32 bit IEEE 754 format.
The first bit is reserved for the sign of the number. Since the number is positive, the first bit is 0
The next 8 bits (2nd to 9th) are reserved for the exponent.
To determine the sign of the exponent, so as not to introduce another sign bit, add a half-byte offset to the exponent +127. So our exponent is: 2 + 127 \u003d 129
Let's translate the exponent into binary representation.
The remaining 23 bits are reserved for the mantissa. For a normalized binary mantissa, the first bit is always 1, since the number lies in the range 1 ≤ M To translate the integer part, you must multiply the digit of the number by the corresponding degree of the digit.
01100000000000000000000 = 2 22 *0 + 2 21 *1 + 2 20 *1 + 2 19 *0 + 2 18 *0 + 2 17 *0 + 2 16 *0 + 2 15 *0 + 2 14 *0 + 2 13 *0 + 2 12 *0 + 2 11 *0 + 2 10 *0 + 2 9 *0 + 2 8 *0 + 2 7 *0 + 2 6 *0 + 2 5 *0 + 2 4 *0 + 2 3 *0 + 2 2 *0 + 2 1 *0 + 2 0 *0 = 0 + 2097152 + 1048576 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 3145728
In decimal code, the mantissa is expressed as the number 3145728
As a result, the number 101.10 represented in IEEE 754 with single precision is.
Let's convert to hexadecimal notation.
Divide source into groups of 4 categories.
2 = 0100 0000 1011 0000 0000 0000 0000 0000 2
We get the number:
0100 0000 1011 0000 0000 0000 0000 0000 2 \u003d 40B00000 16
Real numbers (as opposed to integers) in computer technology are numbers that have a fractional part.
When writing them instead of a comma, it is customary to write a period... So, for example, the number 5 is an integer, and the numbers 5.1 and 5.0 are real.
For the convenience of displaying numbers that take values \u200b\u200bfrom a fairly wide range (that is, both very small and very large), the number notation form is used with base order... For example, the decimal number 1.25 can be represented in this form as follows:
1.25*10 0 = 0.125*10 1 = 0.0125*10 2 = ... ,
or like this:
12.5*10 -1 = 125.0*10 -2 = 1250.0*10 -3 = ... .
If the "floating" point is located in the mantissa before the first significant digit, then with a fixed number of digits allocated for the mantissa, the maximum number of significant digits of the number is recorded, that is, the maximum precision of the number representation in the machine. Therefore:
Such, the most advantageous for a computer, representation of real numbers is called normalized.
It is customary to write the mantissa and the order of a q-ary number in the base q system, and the base itself in the decimal system.
Examples of normalized representation:
Decimal system Binary system
753.15 \u003d 0.75315 * 10 3; -101.01 \u003d -0.10101 * 2 11 (order 11 2 \u003d 3 10)
0.000034 \u003d -0.34 * 10 -4; -0.000011 \u003d 0.11 * 2 -100 (order -100 2 \u003d -410)
Real numbers are written differently in computers of different types. In this case, the computer usually provides the programmer with the opportunity to choose from several number formats that are most suitable for specific task - using four, six, eight or ten bytes.
As an example, here are the characteristics of the real number formats used by IBM-compatible personal computers:
| Real number formats | Size in bytes | Approximate range of absolute values | Number of significant decimal digits |
| Single | 4 | 10 -45 ... 10 38 | 7 or 8 |
| Real | 6 | 10 -39 ... 10 38 | 11 or 12 |
| Double | 8 | 10 -324 ... 10 308 | 15 or 16 |
| Extended | 10 | 10 -4932 ... 10 4932 | 19 or 20 |
From this table it can be seen that the form of representation of floating point numbers allows you to write numbers with high precision and from a very wide range.
When storing floating point numbers, digits for mantissa, order, sign of number and sign of order:
Let's show with examples how some numbers are written in normalized form in a four-byte format with seven order bits.
1. Number 6.25 10 \u003d 110.01 2 \u003d 0.11001
- 2 11:
2. Number -0.125 10 \u003d -0.0012 \u003d -0.1 * 2 -10 (negative order is written in the complement code):
Theme: Representation of numbers in the computer. Fixed and floating point format. Forward, reverse and complementary code.
Reiteration: Converting integers to binary:
13 10 = and 2 Similarly:
13 10 =1101 2
1345 10 =10101000001 2
The representation of integers in the computer.
All information processed by computers is stored in binary form. How is this storage carried out?
Information entered into a computer and arising in the course of its work is stored in its memory. Computer memory can be thought of as a long page of separate lines. Each such line is called memory cell .
Cell - this is a part of the computer's memory that contains information available for processing a separate team processor. The minimum addressable memory cell is called a byte - 8 binary bits. Byte ordinal is called it address .
cell (8bit \u003d 1byte)machine word.
A memory cell consists of a number of homogeneous elements. Each element is capable of being in one of two states and serves to display one of the digits of the number. That is why each cell element is called discharge ... The numbering of the digits in the cell is usually carried out from right to left, the rightmost digit has serial number 0. This is the least significant bit of the memory cell, the most significant bit has a sequence number (n-1) in an n-bit memory cell.
The content of any bit can be either 0 or 1.
The contents of the memory cell are called machine word. The memory cell is divided into bits, each of which stores the digit of the number.
For example, the most modern personal computers are 64-bit, that is, a machine word and, accordingly, a memory cell, consists of 64 bits, or bits.
Bit - the minimum unit of measurement of information. Each bit can be 0 or 1. Bit also called discharge computer memory cells.
Standard size the smallest memory location is eight bits, that is, eight binary digits. A collection of 8 bits is the basic unit of data representation - a byte.
Byte (from English byte - syllable) - a part of a machine word, consisting of 8 bits, processed in a computer as a whole. On the screen, a memory cell consisting of 8 bits is a byte. The least significant bit has sequence number 0, the most significant bit has sequence number 7.
8 bits \u003d 1 byte
Two formats are used to represent numbers in computer memory: fixed point format and floating point format . In fixed-point format, only integers , in floating point format - real numbers (fractional).
In the overwhelming majority of problems solved with a computer, many actions are reduced to operations on integers. This includes tasks of an economic nature, in the solution of which the data is the number of shares, employees, parts, vehicles, etc. Integers are used to indicate the date and time, and to number various objects: array elements, database records, machine addresses, etc.
Integers can be represented in a computer with a sign or unsigned (be positive or negative).
Unsigned integers usuallyoccupy one or two bytes in memory and accept values \u200b\u200bfrom 00000000 in single-byte format 2 up to 11111111 2 , and in double-byte format - from 00000000 00000000 2 up to 11111111 11111111 2 .
Signed integers usually occupy one, two or four bytes in computer memory, while the leftmost (most significant) bit contains information about the sign of the number. The plus sign is coded as zero, and the minus sign is coded by one.
1101 2 10101000001 2The category assigned to the sign
(in this case +)
The most significant bits missing to a whole byte are filled with zeros.
In computer technology, three forms of writing (encoding) signed integers are used:straight the code , back the code , additional the code .
Direct code Is a representation of a number in the binary number system, with the first digit assigned to the number sign. If the number is positive, then the first digit contains 0, if the number is negative, the first digit indicates one.
In fact, straight code is used almost exclusively for positive numbers.To write a direct number code, you must:
Binary number
Supplement the number with zeros to the penultimate most significant bit of an 8-bit or 16-bit cell
Fill in the most significant digit with zero or one, depending on the sign of the number.
Example:number 3 10 in a single-byte format direct code will be represented as:
hislo -3 10 in the direct code of a single-byte format is:
Reverse code for a positive number in the binary system is the same as the direct code. For a negative number, all digits of the number are replaced by their opposite (1 to 0, 0 to 1)invert, and one is entered in the sign bit.
For negative numbers, the so-called complementary code is used. This is due to the convenience of performing operations on numbers by computers.
Additional code used mainly to represent negative numbers in a computer. Such code makes arithmetic operations more convenient for computing.
In two's complement code, as well as in direct, the first digit is reserved to represent the sign of a number. The forward and complement codes for positive numbers are the same. Since the direct code is used almost exclusively to represent positive numbers, and the complementary code is used for negative ones, then almost always, if the first bit is 1, then we are dealing with complementary code. (Zero represents a positive number and one represents a negative number.)
Algorithm for obtaining a complementary code for a negative number:
1. Find the direct code of a number (convert a number to the binary number system unsigned number)
2. Get the reverse code. Change every zero to one and one to zero (invert the number)
3. Add 1 to the reverse code
Example: Find the complementary decimal code - 47 in 16-bit format.
Let's find the binary representation of the number 47 (direct code).
Important!
For positive numbers, the forward, backward and complementary codes are the same, i.e. straight code. There is no need to invert positive numbers for representation in a computer!
Why is it usedadditional code to represent a negative number?
This makes it easier to perform mathematical operations. For example, we have two numbers represented in straight code. One number is positive, the other is negative, and these numbers need to be added. However, you cannot simply fold them. First, the computer must determine what those numbers are. Having found out that one number is negative, he should replace the addition operation with the subtraction operation. Then, the machine must determine which number is greater in absolute value in order to find out the sign of the result and decide on what to subtract from what. As a result, a complex algorithm is obtained. It is much easier to add numbers if the negative ones are converted to two's complement.
Practical task:
Exercise 1. Write the forward, backward, and complementary codes of the next decimal numbers using8-bit cell:
64 10, - 120 10
Task 2. Write forward, backward, and complementary codes for the next decimal numbers in a 16-bit grid
57 10 - 117 10 - 200 10
The maximum value of a non-negative integer is reached when all cells contain ones. For n-bit representation, it will be
non-negative integers... The minimum number corresponds to eight zeros stored in eight bits of the memory cell and is zero. The maximum number corresponds to eight units and is
A \u003d 1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 1 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0 \u003d 1 × 2 8 - 1 \u003d 255 ten .
Range of change non-negative integers numbers: from 0 to 255.
For storage signed integers two memory cells (16 bits) are allocated, and the most significant (left) bit is assigned under the sign of the number (if the number is positive, then 0 is written in the sign bit, if the number is negative - 1).
The computer representation of positive numbers using the sign-magnitude format is called direct code numbers. For example, 2002 10 \u003d 11111010010 2 would be represented in 16-bit form as follows:
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
The maximum positive number (taking into account the allocation of one digit per sign) for signed integers in n-bit representation is:
To represent negative numbers, use additional code... Additional code allows you to replace the arithmetic operation of subtraction with an addition operation, which greatly simplifies the processor's work and increases its performance.
The complement code of a negative number A stored in n cells is 2 n - | A |.
The complement code is the complement of the modulus of a negative number A to 0, since in n-bit computer arithmetic:
2 n - | A | + | A | \u003d 0,
since in computer n-bit arithmetic 2 n \u003d 0. Indeed, the binary notation of such a number consists of one one and n zeros, and an n-bit cell can only fit n least significant bits, that is, n zeros.
A rather simple algorithm can be used to get the complementary code for a negative number:
1. Write the module of the number in direct code in n binary digits.
2. Get reverse code numbers, for this, the values \u200b\u200bof all bits are inverted (replace all ones with zeros and replace all zeros with ones).
3. Add one to the received reverse code.
Let's write the additional code for a negative number -2002 for a 16-bit computer representation:
 |
In the n-bit representation of a negative number A in two's complement, the most significant bit is allocated to store the sign of the number (one). The rest of the digits contain a positive number
For the number to be positive, the condition must be met
| A | £ 2 n-1.
Therefore, the maximum value of the absolute value of the number A in the g-bit representation is:
Then the minimum negative number is:
Let's define the range of numbers that can be stored in RAM in the format long signed integers (for storing such numbers, four memory cells are allocated - 32 bits).
The maximum positive integer (taking into account the allocation of one digit per sign) is:
A \u003d 2 31 - 1 \u003d 2 147 483 647 10.
The minimum negative integer is:
A \u003d -2 31 \u003d - 2 147 483 648 10.
The advantages of representing numbers in c format fixed point are the simplicity and clarity of the representation of numbers, as well as the simplicity of algorithms for the implementation of arithmetic operations.
The disadvantage of representing numbers in c fixed point is a small range of representation of quantities, insufficient for solving mathematical, physical, economic and other problems in which both very small and very large numbers are used.
Floating point representation of numbers. Real numbers are stored and processed in a computer in the format floating point... In this case, the position of the comma in the number record may change.
Number format floating point is based on exponential notation, in which any number can be represented. So the number A can be represented as:
| A \u003d m × q n | 2.3 |
where m is the mantissa of the number;
q - base of the number system;
n is the order of the number.
For consistency in the representation of numbers floating point the normalized form is used, in which the mantissa meets the condition:
1 / n £ | m |
This means that the mantissa must be a regular fraction and have a nonzero digit after the decimal point.
Convert the decimal number 555.55, written in natural form, to exponential form with a normalized mantissa:
555.55 \u003d 0.55555 × 10 3.
Here is the normalized mantissa: m \u003d 0.55555, order: n \u003d 3.
A floating point number occupies 4 ( ordinary precision number) or 8 bytes ( double precision number). When writing a floating point number, bits are allocated to store the sign of the mantissa, sign of order, order and mantissa.
The range of numbers is determined by the number of digits allocated to store the order of the number, and the precision (the number of significant digits) is determined by the number of digits allocated to store the mantissa.
Determine the maximum number and its precision for the format ordinary precision numbersif 8 bits are allocated for storing the order and its sign, and 24 bits for storing the mantissa and its sign:
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| sign and order | sign and mantissa | ||||||||||||||||||||||
The maximum value of the order of number will be 1111111 2 \u003d 127 10, and therefore the maximum value of the number will be:
2 127 \u003d 1.7014118346046923173168730371588 × 10 38.
The maximum value of the positive mantissa is:
2 23 - 1 "2 23 \u003d 2 (10 × 2.3)" 1000 2.3 \u003d 10 (3 × 2.3) "10 7.
Thus, the maximum value ordinary precision numbers taking into account the possible accuracy of calculations, it will be 1.701411 × 10 38 (the number of significant digits of the decimal number in this case is limited to 7 digits).
Tasks
1.26. Populate the table by writing negative forward, backward and two's complement decimal numbers in 16-bit notation:
1.27. Define presentation range signed integers (2 bytes of memory allocated) in fixed point format.
1.28. Determine the maximum number and its precision for the format double precision numbersif 11 bits are allocated for storing the order and its sign, and 53 bits for storing the mantissa and its sign.
Numerical data is processed in a computer in a binary number system. Numbers are stored in the computer memory in binary code, that is, as a sequence of zeros and ones, and can be represented in fixed or floating point format.
Integers are stored in memory in fixed point format. With this format for representing numbers, a memory register consisting of eight memory cells (8 bits) is allocated to store non-negative integers. Each bit of the memory cell always corresponds to the same bit of the number, and the comma is on the right after the least significant bit and outside the bit grid. For example, the number 110011012 will be stored in a memory register as follows:
Table 4
The maximum value of a non-negative integer number that can be stored in a register in fixed-point format can be determined from the formula: 2n - 1, where n is the number of digits of the number. The maximum number in this case will be equal to 28 - 1 \u003d 25510 \u003d 111111112 and the minimum 010 \u003d 000000002. Thus, the range of variation of non-negative integers will be in the range from 0 to 25510.
In contrast to the decimal system, in the binary system, the computer representation of a binary number does not have symbols that indicate the sign of a number: positive (+) or negative (-), therefore, two formats for representing numbers are used to represent signed integers in the binary system: the format of the value of the number signed and complementary code format. In the first case, two memory registers (16 bits) are allocated to store signed integers, and the most significant bit (the leftmost one) is used under the sign of the number: if the number is positive, then 0 is written in the signed bit, if the number is negative, then - 1. For example , number 53610 \u003d 00000010000110002 will be represented in memory registers in the following form:
Table 5
and a negative number -53610 \u003d 10000010000110002 in the form:
Table 6
The maximum positive number or minimum negative in the signed number format (taking into account the representation of one digit under the sign) is 2n-1 - 1 \u003d 216 - 1 - 1 \u003d 215 - 1 \u003d 3276710 \u003d 1111111111111112 and the range of numbers will be in the range from - 3276710 to 32767.
Most often, to represent signed integers in the binary system, the complement code format is used, which allows you to replace the arithmetic operation of subtraction in a computer with an addition operation, which greatly simplifies the structure of the microprocessor and increases its performance.
To represent negative integers in this format, use's complement code, which is the modulus of a negative number's complement to zero. Converting a negative integer number into a complementary code is carried out using the following operations:
1) write the module of the number in direct code in n (n \u003d 16) binary digits;
2) get the reverse code of the number (invert all digits of the number, that is, replace all ones with zeros, and zeros with ones);
3) to the received reverse code add one to the least significant digit.
For example, for the number -53610 in this format, the modulus will be 00000010000110002, the reverse code is 1111110111100111, and the additional code is 1111110111101000.
It must be remembered that the complementary code of a positive number is the number itself.
For storing signed integers other than 16-bit computer representation when used two memory registers (this number format is also referred to as the signed short integer format), the signed medium and long integer formats are used. Four registers are used to represent numbers in the format of middle numbers (4 x 8 \u003d 32 bits), and to represent numbers in the format of long numbers, eight registers (8 x 8 \u003d 64 bits). The ranges of values \u200b\u200bfor the format of medium and long numbers will be respectively: - (231 - 1)… + 231 - 1 and - (263-1)… + 263 - 1.
Computer representation of numbers in fixed point format has advantages and disadvantages. TO advantages the simplicity of the representation of numbers and algorithms for the implementation of arithmetic operations are related, the disadvantages are the finite range of representation of numbers, which may be insufficient for solving many problems of a practical nature (mathematical, economic, physical, etc.).
Real numbers (finite and infinite decimal fractions) are processed and stored in the computer in floating point format. With this format for representing the number, the position of the comma in the record can change. Any real number K in floating point format can be represented as:
where A is the mantissa of the number; h - base of the number system; p is the order of the number.
Expression (2.7) for the decimal number system will take the form:
![]()
for binary -
![]()
for octal -
![]()
for hexadecimal -
![]()
This form of number representation is also called normal ... With a change in the order, the comma in the number shifts, that is, it seems to float to the left or right. Therefore, the normal form of representation of numbers is called floating point... Decimal number 15.5, for example, in floating point format can be represented as: 0.155 · 102; 1.55 * 101; 15.5 * 100; 155.0 * 10-1; 1550.0 10-2, etc. This form of writing the decimal number 15.5 with floating point is not used when writing computer programs and entering them into a computer (input devices of computers perceive only linear data recording). Based on this, expression (2.7) for representing decimal numbers and entering them into a computer is converted to the form
where P is the order of the number,
that is, instead of the base of the number system 10, they write the letter E, instead of a comma - a point, and the multiplication sign is not put. Thus, the number 15.5 in floating point format and linear notation (computer representation) will be written as: 0.155Е2; 1.55E1; 15.5E0; 155.0E-1; 1550.0Е-2, etc.
Regardless of the number system, any floating-point number can be represented by an infinite number of numbers. This form of notation is called unnormalized ... For an unambiguous representation of floating point numbers, the normalized form of notation is used, in which the mantissa of the number must meet the condition
where | A | - the absolute value of the mantissa of the number.
Condition (2.9) means that the mantissa must be a regular fraction and have a nonzero digit after the decimal point, or, in other words, if there is a nonzero after the decimal point in the mantissa, then the number is called normalized. So, the number 15.5 in normalized form (normalized mantissa) in floating point form will look like this: 0.155102, that is, the normalized mantissa will be A \u003d 0.155 and order P \u003d 2, or in the computer representation of the number 0.155E2 ...
Floating point numbers have a fixed format and occupy four (32 bits) or eight bytes (64 bits) in computer memory. If a number occupies 32 bits in the computer's memory, then this is a normal precision number, if 64 bits, then this is a double precision number. When writing a floating point number, bits are allocated to store the sign of the mantissa, sign of the order, mantissa and order. The number of digits that are allocated for the order of the number determines the range of changes in numbers, and the number of digits allocated for storing the mantissa determines the precision with which the number is specified.
When performing arithmetic operations (addition and subtraction) on numbers represented in floating point format, the following procedure (algorithm) is implemented:
1) alignment of the orders of numbers is performed on which arithmetic operations are performed (the order of the number smaller in absolute value increases to a value of the order of the number greater in absolute value, while the mantissa decreases by the same number of times);
2) arithmetic operations are performed on the mantissa of numbers;
3) the result is normalized.
Practical part